10th Class math’s solution Chapter 1.4

 

10th Class math’s solution Chapter 1

CERT Solutions For Class 10 Maths Chapter 1 Real Numbers Ex1.4

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 1.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 1.4

Access Answers of Math's NCERT Class 10 Chapter 1 – Real Number Exercise 1.4

1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating decimal expansion.

(i)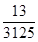 

(ii)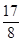 

(iii)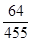 

(iv)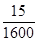 

(v)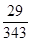 

(vi)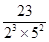 

(vii)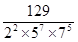 

(viii)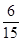 

(ix)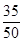 

(x)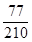 

Ans. According to Theorem, any given rational number of the form 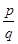where p and q are co-prime, has a terminating decimal expansion if q is of the form 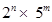, where m and n are non-negative integers.

(i)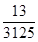 

q = 3125 =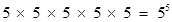 

Here, denominator is of the form 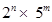, where m = 5 and n = 0.

It means rational number 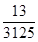 has a terminating decimal expansion.

(ii)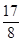 

q = 8 =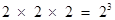 

Here, denominator is of the form 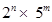, where m = 0 and n = 3.

It means rational number 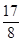 has a terminating decimal expansion.

(iii)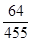 

q = 455 =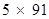 

Here, denominator is not of the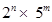, where m and n are non-negative integers.

It means rational number 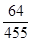 has a non-terminating repeating decimal expansion.

(iv)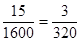 

q = 320 = =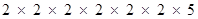 

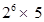
Here, denominator is of the form 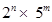, where m = 1 and n = 6.

It means rational number 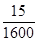 has a terminating decimal expansion.

(v)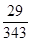 

q = 343 =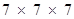 

Here, denominator is not of the form 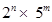, where m and n are non-negative integers.

It means rational number 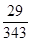 has non-terminating repeating decimal expansion.

(vi)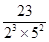 

q =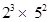 

Here, denominator is of the form 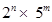, where m = 2 and n = 3 are non-negative integers.

It means rational number 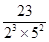 has terminating decimal expansion.

(vii)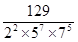 

q =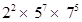 

Here, denominator is not of the form 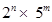, where m and n are non-negative integers.

It means rational number 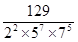 has non-terminating repeating decimal expansion.

(viii)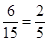 

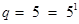
Here, denominator is of the form 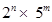, where m = 1 and n = 0.

It means rational number 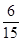 has terminating decimal expansion.

(ix)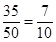 

q = 10 =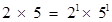 

Here, denominator is of the form 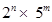, where m = 1 and n = 1.

It means rational number 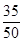 has terminating decimal expansion.

(x)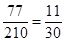 

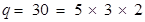
Here, denominator is not of the form 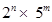, where m and n are non-negative integers.

It means rational number 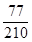 has non-terminating repeating decimal expansion.

---

NCERT Solutions for Class 10 Maths Exercise 1.4

2. Write down the decimal expansions of those rational numbers in Question 1 which have terminating decimal expansions.

Ans. (i)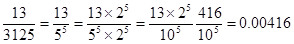 

(ii)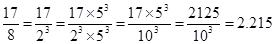 

(iv)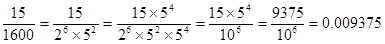 

(vi)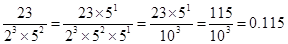 

(viii)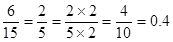 

(ix)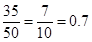 

3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If, they are rational, and of the form 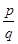, what can you say about the prime factors of q?

(i) 43.123456789

(ii) 0.1201120012000120000…

(iii)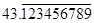 

Ans. (i) 43.123456789

It is rational because decimal expansion is terminating. Therefore, it can be expressed in 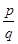 form where factors of q are of the form 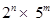where n and m are non-negative integers

(ii) 0.1201120012000120000…

It is irrational because decimal expansion is neither terminating nor non-terminating repeating.

(iii)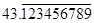 

It is rational because decimal expansion is non-terminating repeating. Therefore, it can be expressed in 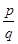 form where factors of q are not of the form 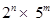where n and m are non-negative integers.

Class 10 Maths Real Numbers

Rational numbers and irrational numbers are taken together form the set of real numbers. The set of real numbers is denoted by R. Thus every real number is either a rational number or an irrational number. In either case, it has a non–terminating decimal representation. In the case of rational numbers, the decimal representation is repeating (including repeating zeroes) and if the decimal representation is non–repeating, it is an irrational number. For every real number, there corresponds a unique point on the number line ‘l’ or we may say that every point on the line ‘l’ corresponds to a real number (rational or irrational).

From the above discussion we may conclude that:
To every real number there corresponds a unique point on the number line and conversely, to every point on the number line there corresponds a real number. Thus we see that there is one–to–one correspondence between the real numbers and points on the number line ‘l’, that is why the number line is called the ‘real number line’